Macau Tutorial¶
In these examples we use ChEMBL dataset for compound-proteins activities (IC50). The IC50 values and ECFP fingerprints can be downloaded from these two urls:
wget http://homes.esat.kuleuven.be/~jsimm/chembl-IC50-346targets.mm
wget http://homes.esat.kuleuven.be/~jsimm/chembl-IC50-compound-feat.mm
Matrix Factorization Model¶
The matrix factorization models cell Y[i,j] by the inner product of the latents
where \(\mathbf{u}_i\) and \(\mathbf{v}_j\) are the latent vector for i-th row and j-th column, and \(\alpha\) is the precision of the observation noise. The model also uses a fixed global mean for the whole matrix.
Matrix Factorization with Side Information¶
In this example we use MCMC (Gibbs) sampling to perform factorization of the compound x protein IC50 matrix by using ECFP features as side information on the compounds.
import macau
import scipy.io
## loading data
ic50 = scipy.io.mmread("chembl-IC50-346targets.mm")
ecfp = scipy.io.mmread("chembl-IC50-compound-feat.mm")
## running factorization (Macau)
result = macau.macau(Y = ic50,
Ytest = 0.2,
side = [ecfp, None],
num_latent = 32,
precision = 5.0,
burnin = 400,
nsamples = 1600)
Input matrix for Y is a sparse scipy matrix (either coo_matrix, csr_matrix or csc_matrix).
In this example, we have assigned 20% of the IC50 data to the test set by setting Ytest = 0.2.
If you want to use a predefined test data, set Ytest = my_test_matrix, where the matrix is a sparse matrix of the same size as Y.
Here we have used burn-in of 400 samples for the Gibbs sampler and then collected 1600 samples from the model.
This is usually sufficient. For quick runs smaller numbers can be used, like burnin = 100, nsamples = 500.
The parameter side = [ecfp, None] sets the side information for rows and columns, respectively.
In this example we only use side information for the compounds (rows of the matrix).
The precision = 5.0 specifies the precision of the IC50 observations, i.e., 1 / variance.
When the run has completed you can check the result object and its prediction field, which is a Pandas DataFrame.
>>> result
Matrix factorization results
Test RMSE: 0.6393
Matrix size: [15073 x 346]
Number of train: 47424
Number of test: 11856
To see predictions on test set see '.prediction' field.
>>> result.prediction
col row y y_pred y_pred_std
0 0 2233 5.7721 5.750984 1.177526
1 0 2354 5.0947 5.379610 0.857858
...
Univariate sampler¶
Macau also includes an option to use a very fast univariate sampler, i.e., instead of sampling blocks of variables jointly it samples each individually. An example:
import macau
import scipy.io
## loading data
ic50 = scipy.io.mmread("chembl-IC50-346targets.mm")
ecfp = scipy.io.mmread("chembl-IC50-compound-feat.mm")
## running factorization (Macau)
result = macau.macau(Y = ic50,
Ytest = 0.2,
side = [ecfp, None],
num_latent = 32,
precision = 5.0,
univariate = True,
burnin = 500,
nsamples = 3500)
When using it we recommend using larger values for burnin and nsamples, because the univariate sampler mixes slower than the blocked sampler.
Adaptive noise¶
In the previous examples we fixed the observation noise by specifying precision = 5.0.
Instead we can also allow the model to automatically determine the precision of the noise by setting precision = “adaptive”.
import macau
import scipy.io
## loading data
ic50 = scipy.io.mmread("chembl-IC50-346targets.mm")
ecfp = scipy.io.mmread("chembl-IC50-compound-feat.mm")
## running factorization (Macau)
result = macau.macau(Y = ic50,
Ytest = 0.2,
side = [ecfp, None],
num_latent = 32,
precision = "adaptive",
univariate = True,
burnin = 500,
nsamples = 3500)
In the case of adaptive noise the model updates (samples) the precision parameter in every iteration, which is then also shown in the output.
Additionally, there is a parameter sn_max that sets the maximum allowed signal-to-noise ratio.
This means that if the updated precision would imply a higher signal-to-noise ratio than sn_max, then the precision value is set to (sn_max + 1.0) / Yvar where Yvar is the variance of the training dataset Y.
Binary matrices¶
Macau can also factorize binary matrices (with or without side information). As an input the sparse matrix should only contain values of 0 or 1.
To factorize them we employ probit noise model that can be enabled by precision = “probit”.
Care has to be taken to make input to the model, as operating with sparse matrices can drop real 0 measurements. In the below example, we first copy the matrix (line 9) and then threshold the data to binary (line 10).
Currently, the probit model only works with the multivariate sampler (univariate = False).
import macau
import scipy.io
## loading data
ic50 = scipy.io.mmread("chembl-IC50-346targets.mm")
ecfp = scipy.io.mmread("chembl-IC50-compound-feat.mm")
## using activity threshold pIC50 > 6.5
act = ic50
act.data = act.data > 6.5
## running factorization (Macau)
result = macau.macau(Y = act,
Ytest = 0.2,
side = [ecfp, None],
num_latent = 32,
precision = "probit",
univariate = False,
burnin = 400,
nsamples = 1600)
Matrix Factorization without Side Information¶
To run matrix factorization without side information you can just drop the side parameter.
result = macau.macau(Y = ic50,
Ytest = 0.2,
num_latent = 32,
precision = 5.0,
burnin = 200,
nsamples = 800)
Without side information Macau is equivalent to standard Bayesian Matrix Factorization (BPMF). However, if available using side information can significantly improve the model accuracy. In the case of IC50 data the accuracy improves from RMSE of 0.90 to close to 0.60.
Tensor Factorization¶
Macau also supports tensor factorization with and without side information on any of the modes.
Tensor can be thought as generalization of matrix to relations with more than two items.
For example 3-tensor of drug x cell x gene could express the effect of a drug on the given cell and gene.
In this case the prediction for the element Yhat[i,j,k] is given by
Visually the model can be represented as follows:
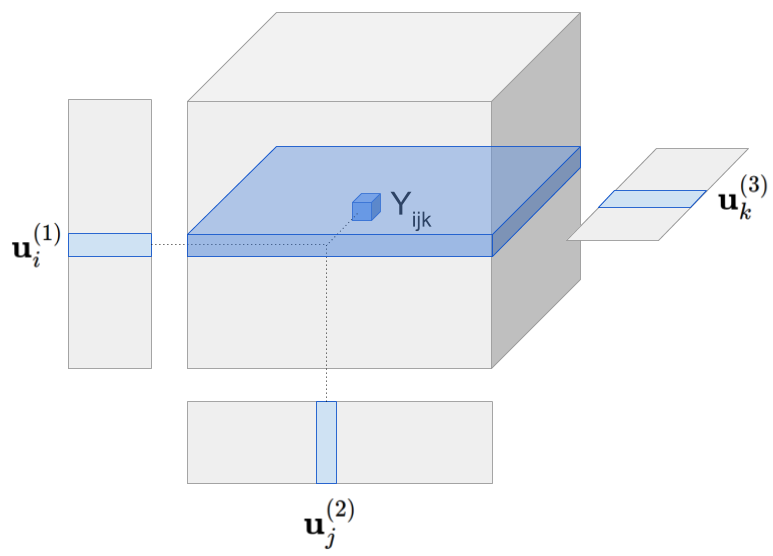
Tensor model predicts Yhat[i,j,k] by multiplying all latent vectors together element-wise and then taking the sum along the latent dimension (figure omits the global mean).
For tensors Macau packages uses Pandas DataFrame where each row stores the coordinate and the value of a known
cell in the tensor.
Specifically, the integer columns in the DataFrame give the coordinate of the cell and float (or double) column
stores the value in the cell (the order of the columns does not matter).
The coordinates are 0-based.
Here is a simple toy example with factorizing a 3-tensor with side information on the first mode.
import numpy as np
import pandas as pd
import scipy.sparse
import macau
import itertools
## generating toy data
A = np.random.randn(15, 2)
B = np.random.randn(3, 2)
C = np.random.randn(2, 2)
idx = list( itertools.product(np.arange(A.shape[0]),
np.arange(B.shape[0]),
np.arange(C.shape[0])) )
df = pd.DataFrame( np.asarray(idx), columns=["A", "B", "C"])
df["value"] = np.array([ np.sum(A[i[0], :] * B[i[1], :] * C[i[2], :]) for i in idx ])
## side information is again a sparse matrix
Acoo = scipy.sparse.coo_matrix(A)
## assigning 20% of the cells to test set
Ytrain, Ytest = macau.make_train_test_df(df, 0.2)
## for artificial dataset using small values for burnin, nsamples and num_latents is fine
results = macau.macau(Y = Ytrain, Ytest = Ytest, side=[Acoo, None, None], num_latent = 4,
verbose = True, burnin = 20, nsamples = 20,
univariate = False, precision = 50)
The side informatoin added here is very informative, thus, using it will significantly increase
the accuracy. The factorization can be executed also without the side information by removing
side=[Acoo, None, None]:
## tensor factorization without side information
results = macau.macau(Y = Ytrain, Ytest = Ytest, num_latent = 4,
verbose = True, burnin = 20, nsamples = 20,
univariate = False, precision = 50)
Tensor factorization also supports the univariate sampler. To execute that set univariate = True, for example
results = macau.macau(Y = Ytrain, Ytest = Ytest, side=[Acoo, None, None], num_latent = 4,
verbose = True, burnin = 20, nsamples = 20,
univariate = True, precision = 50)